Are you ready to dive deep into the world of tangent unit circle? It’s not just some random math term; it’s the key to unlocking advanced trigonometry concepts. Whether you’re a student trying to ace your exams or someone brushing up on their math skills, understanding the tangent unit circle is crucial. So, buckle up, because we’re about to break it down in a way that’s as easy as pie.

Now, let’s face it, math can be intimidating. But don’t worry, we’ve got your back. The tangent unit circle might sound complex, but once you get the hang of it, you’ll realize how simple and logical it is. Think of it as a map for navigating angles and their corresponding tangents. And who doesn’t love a good map, right?

This article is designed to help you grasp the concept of the tangent unit circle in a way that’s both fun and informative. We’ll cover everything from the basics to advanced applications, so whether you’re a beginner or a math enthusiast, there’s something here for everyone. Let’s get started!

Read also:
Gary Plauche Video The Ultimate Guide To His Work And Legacy

What is the Tangent Unit Circle?

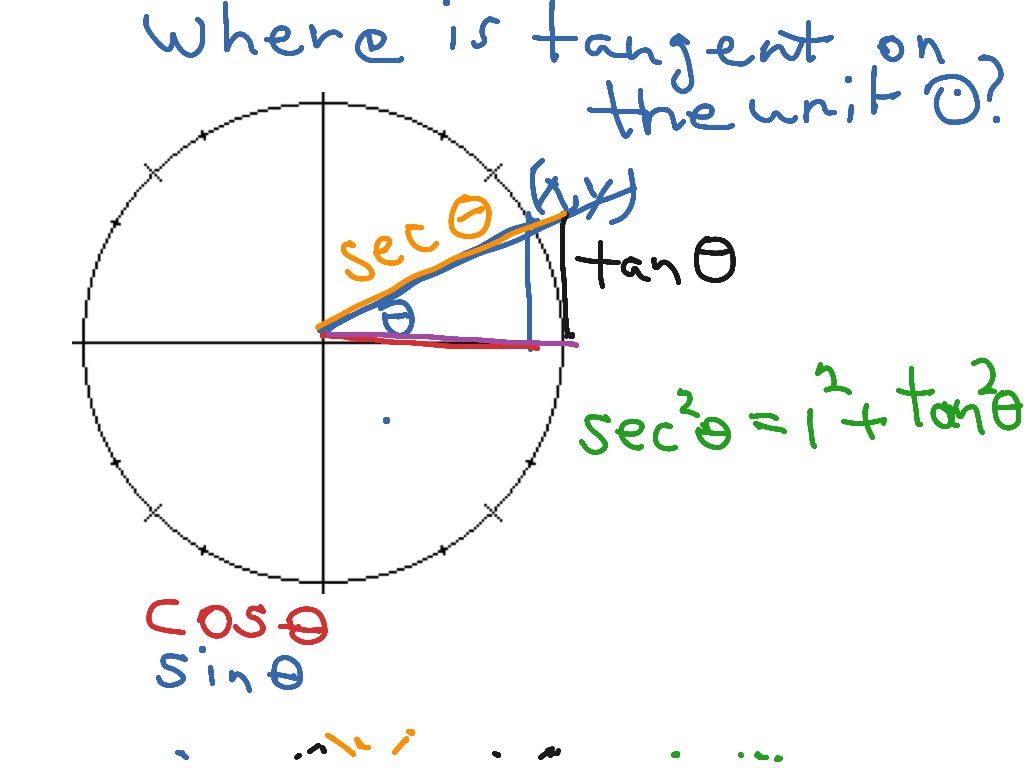
The tangent unit circle is basically an extension of the unit circle, but with a twist. It focuses on the tangent function, which is one of the main trigonometric functions. If you’re familiar with sine and cosine, think of tangent as their cool cousin. The tangent function is defined as the ratio of sine to cosine, and the unit circle helps visualize this relationship.

Why Does the Tangent Unit Circle Matter?

Here’s the deal: the tangent unit circle isn’t just a theoretical concept. It has real-world applications in fields like engineering, physics, and even computer graphics. For example, when designing roller coasters or calculating the trajectory of a rocket, engineers rely on trigonometric functions, including the tangent. So, understanding this concept isn’t just about passing a test; it’s about understanding how the world works.

Breaking Down the Unit Circle

Before we dive into the tangent unit circle, let’s revisit the basics of the unit circle. The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane. It’s like the foundation of trigonometry, where every point on the circle corresponds to an angle and its sine and cosine values.

Key Points on the Unit Circle

The unit circle covers angles from 0 to 360 degrees (or 0 to 2π radians).
Each angle has corresponding sine and cosine values.
Quadrants divide the circle into four sections, each with unique characteristics.

Understanding these basics is essential before moving on to the tangent unit circle. Think of it as building a strong foundation before adding the fancy decorations.

Tangent Function: The Star of the Show

So, what exactly is the tangent function? In simple terms, it’s the ratio of sine to cosine. Mathematically, it’s expressed as tan(θ) = sin(θ) / cos(θ). But what does that mean in practice? Well, the tangent function tells us the slope of the line at a given angle. It’s like the slope of a hill; some angles have steep slopes, while others are more gradual.

How Tangent Relates to the Unit Circle

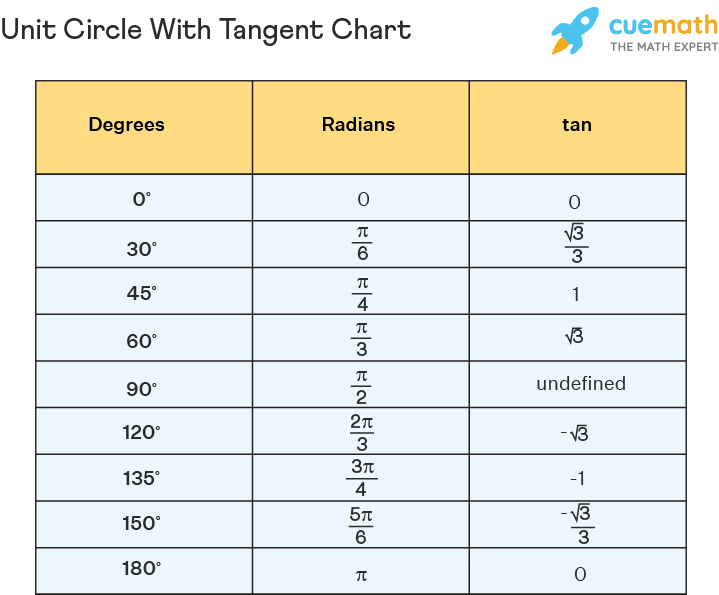
When we talk about the tangent unit circle, we’re essentially mapping out the tangent values for every angle on the unit circle. This creates a visual representation of how the tangent function behaves. For example, at 0 degrees, the tangent is 0, and at 45 degrees, it’s 1. But as you move closer to 90 degrees, the tangent value shoots up to infinity. Crazy, right?

Read also:
Ronald Logan Delphi Indiana Unveiling The Truth Behind The Headlines

Exploring Quadrants and Tangent Values

One of the coolest things about the tangent unit circle is how it behaves in different quadrants. Each quadrant has its own set of rules, and understanding these rules is key to mastering the concept.

Quadrant I: The Happy Zone

In Quadrant I, both sine and cosine are positive, so the tangent is also positive. This means the slopes are upward and gentle. It’s like cruising downhill on a bike—smooth and easy.

Quadrant II: Where Things Get Interesting

Move to Quadrant II, and things start to change. Here, sine is positive, but cosine is negative, making the tangent negative. The slopes are downward, indicating a reversal in direction. It’s like riding uphill; you’re working against gravity.

Quadrant III: The Dark Side

In Quadrant III, both sine and cosine are negative, so the tangent is positive again. This creates upward slopes, but with a twist—they’re steeper than in Quadrant I. It’s like navigating a steep hill; you’re still moving up, but it’s more challenging.

Quadrant IV: Back to Normal

Finally, in Quadrant IV, sine is negative, and cosine is positive, making the tangent negative. The slopes are downward again, but less steep than in Quadrant II. It’s like coasting downhill after a tough climb.

Visualizing the Tangent Unit Circle

Now that we’ve covered the basics, let’s talk about how to visualize the tangent unit circle. Imagine a circle with a radius of 1, and draw lines from the origin to various points on the circle. Each line represents an angle, and the slope of the line represents the tangent value. It’s like drawing a map of angles and their corresponding slopes.

Using Graphs to Understand Tangent

Graphs are a great way to visualize the tangent function. When you plot the tangent values against the angles, you’ll notice a pattern. The graph has vertical asymptotes at certain points, indicating where the tangent value becomes infinite. These asymptotes occur at angles where cosine equals zero, like 90 degrees and 270 degrees.

Practical Applications of the Tangent Unit Circle

So, why should you care about the tangent unit circle? Because it’s everywhere! From engineering to physics, the tangent function plays a crucial role in solving real-world problems. Here are a few examples:

Engineering: Engineers use tangent to calculate angles and slopes in structures like bridges and buildings.
Physics: Physicists rely on tangent to analyze motion and forces, especially in projectile motion.
Computer Graphics: Game developers use tangent to create realistic 3D environments and animations.

Real-Life Example: Designing Roller Coasters

Ever wondered how roller coasters are designed? Engineers use trigonometric functions, including tangent, to calculate the angles and slopes of the tracks. By understanding the tangent unit circle, they can ensure a smooth and thrilling ride for passengers.

Tips for Mastering the Tangent Unit Circle

Learning the tangent unit circle can be challenging, but with the right approach, it’s totally doable. Here are a few tips to help you master this concept:

Practice, Practice, Practice: Solve as many problems as you can to reinforce your understanding.
Use Visual Aids: Draw graphs and diagrams to visualize the tangent function.
Memorize Key Angles: Familiarize yourself with common angles and their tangent values.

Common Mistakes to Avoid

Even the best of us make mistakes when learning new concepts. Here are a few common pitfalls to watch out for:

Confusing Quadrants: Make sure you understand how tangent behaves in each quadrant.
Forgetting Asymptotes: Don’t overlook the vertical asymptotes where tangent becomes infinite.
Relying Too Much on Calculators: While calculators are helpful, try to develop an intuitive understanding of the concept.

Conclusion: Unlocking the Power of Tangent Unit Circle

And there you have it—a comprehensive guide to mastering the tangent unit circle. From understanding the basics to exploring real-world applications, we’ve covered it all. Remember, the tangent unit circle isn’t just a math concept; it’s a tool that can help you solve complex problems in various fields.

So, what’s next? Take what you’ve learned and apply it to your studies or work. Practice regularly, and don’t be afraid to ask questions. And most importantly, share this article with your friends and classmates. Together, we can make math less intimidating and more exciting!

Now it’s your turn. Are you ready to embrace the tangent unit circle and take your math skills to the next level? Let us know in the comments below!